Async/await inference in Firefly: Part 2

In the last post, we sketched out the high level rules of the async/await inference. This post will show how it works under the hood for a concrete example. If you missed the last post, here it is:

Async/await inference in Firefly

Firefly is a new general purpose programming language that tries to achieve convenience and safety at the same time, by using pervasive dependency injection. There is no global access to the file system, the network, other processes or devices. Instead, you access these through a system object that…

Ahnfelt.netJoakim Ahnfelt-Rønne

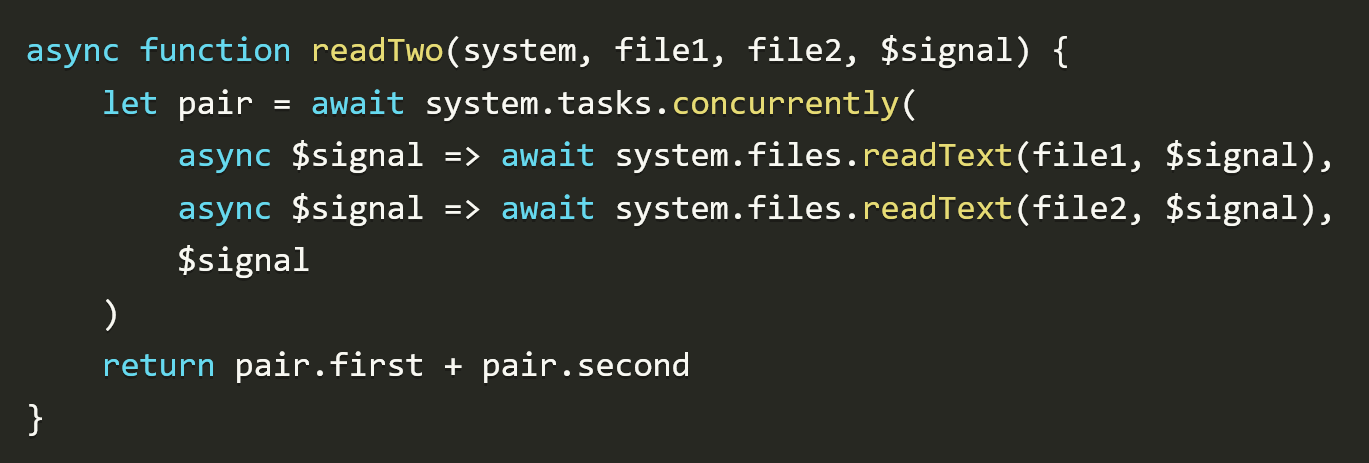
The first example we're going to look at was suggested by MarcoServetto, the author of the 42 programming language. It reads two files concurrently, and then concatenates the result:

readTwo(system: System, file1: String, file2: String): String {
    let pair = system.tasks.concurrently(
        {system.files.readText(file1)},
        {system.files.readText(file2)}
    )
    pair.first + pair.second
}

The curly braces in {system.files.readText(...)} is the syntax for lambda functions in Firefly, in this case just to delay the execution so that concurrently can do its thing. The goal is to infer async/await and transform this into the following JavaScript:

async function readTwo(system, file1, file2) {
    let pair = await system.tasks.concurrently(
        async () => await system.files.readText(file1),
        async () => await system.files.readText(file2)
    )
    return pair.first + pair.second
}

Where concurrently is implemented in terms of Promise.all():

async function concurrently(taskSystem, task1, task2) {
    let array = await Promise.all([task1(), task2()])
    return {first: array[0], second: array[1]}
}

With that out of the way, let's look at how the async/await inference proceeds. For this, we'll need both type equality constraints (unification) and an assymetric type constraint $1 affects $2. You can read up on the former here:

Type Inference by Example

In this series, we’ll go through examples of how type inference works on actual code, and then see how to implement it.

MediumJoakim Ahnfelt-Rønne

So let's begin. The first step in the analysis is to add add an effect parameter to the internal representation every top level function signature, akin to a type parameter. Let's call it E. We'll also add an effect to each signature and call, written !E.

Now, for the sake of keeping things simple, imagine concurrently and readText as top level functions, instead of extension methods (it works the same way). Here's the signature they get internally after the analysis adds the E effect parameter:

concurrently[E, A, B](tasks: TaskSystem[E], first: () =E> A, second: () =E> B): Pair[A, B] !E

readText[E](tasks: TaskSystem[E], file: String): String !E

The effect parameter is added to TaskSystem, because that's a type that may contain async capabilities, and so are function types (I've placed the E on the arrow there). It's not added to String, which may not contain async capabilities.

The analysis then proceeds by adding fresh effect variables $1, $2, $3 to each call inside readTwo:

readTwo[E](system: System[E], file1: String, file2: String): String !E {
    let pair = system.tasks.concurrently[$1, () =$1> String, () =$1> String](
        {system.files.readText[$2](file1) !$2},
        {system.files.readText[$3](file2) !$3}
    ) !$1
    pair.first + pair.second
}

Looking at {system.files.readText[$2](file1) !$2}, that's a lambda function with a call inside. This call has effect $2, and the enclosing lambda has type () =$1> String, so we add $2 affects $1 to our constraints.

Because system.files: System[E], we get $2 = E. For arbitrary x, y, when we bind $2 = x in the substitution, we replace all $2 affects y with x affects y. If the left hand side x of affect is ever bound to E, we bind y to E as well.

Since $2 affects $1 and $2 = E, we can conclude $1 = E. The next line is similar, so $3 = E.

Then looking at the call to concurrently, we already know that $1 = E, so when we substitute the effect variables, we get:

readTwo[E](system: System[E], file1: String, file2: String): String !E {
    let pair = system.tasks.concurrently[E, () =E> String, () =E> String](
        {system.files.readText[E](file1) !E},
        {system.files.readText[E](file2) !E}
    ) !E
    pair.first + pair.second
}

Meaning "the calls on line 2, 3 and 4 are async if E is Async".

Note that any effect variables that has not been unified with E when the bottom of the top level function is reached are considered synchronous.

We now generate two versions of this function: One sync and one async. In this case, we know that the runtime will never construct a sync instance of System, so we could leave the sync version of the function out, or just let tree shaking eliminiate it later.

The async version is generated by inserting async at every function whose effect is !E, and await at every call whose effect is !E:

async function readTwo(system, file1, file2) {
    let pair = await system.tasks.concurrently(
        async () => await system.files.readText(file1),
        async () => await system.files.readText(file2)
    )
    return pair.first + pair.second
}

And we're done.

In the next installment, we'll look at task cancellation and structured concurrency:

Async/await inference in Firefly: Part 3

In the last post, we saw how to implement colorless async/await via effect inference. In this post, we will extend the solution to solve a common problem in web apps, where requests continue on even though the response will never be used. It’s like a memory leak, but one

Ahnfelt.netJoakim Ahnfelt-Rønne